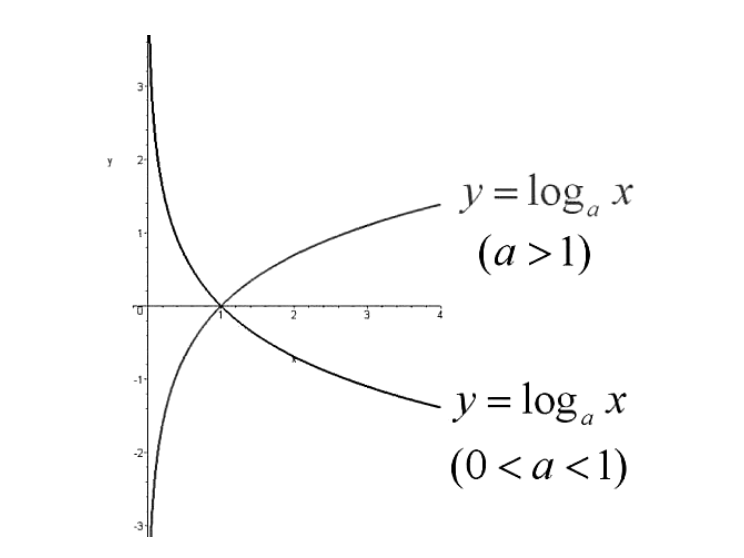对数函数:心心相印于xy轴
复杂恋情的演绎者
对数函数
与男友相识、相知、相恋到分手,让质子失魂落魄......世间的缘分想想真的很神奇,互不相识的异乡人来到同一个陌生城市,因为共同的兴趣喜好而相识相知,携手一路相伴五年时间,最终因为双方家庭观念不和而分手。任凭眼泪流下也唤不回相恋时光,阻挡不了缘分已尽的无奈。
该用什么样的方式才能呈现众多像质子这样的无结局恋情呢?
对数函数便是这么一种唯美生动、能惟妙惟肖地完美演绎这恋情的方式。我想世间唯有这简洁清晰的坐标系语,能够贴切地描述质子与男友合子的复杂恋情了。
与对数函数如出一辙,纵然从开始就有着截然不同的出身起点y,也同样有着广阔的四个象限,却只喜欢在两个领域内发展。拥有同一个安稳而又繁荣的大时代背景log,有着看似形式相同却完全不一样的家庭文化底蕴a,尽管它们有着共同的喜好和梦想X,必然能相会相聚,但因为家境文化底蕴a的不同,一个享受着a>1的得天独厚的优渥条件,一个却只能靠0<a<1的有限资源来打拼,两者终究逃不开分散的命运安排。<>
触发恋情的导火索
混沌之局
混混沌沌的世界里,对数函数等待着开天辟地的造物主。在对数问世之前,群“魔”乱舞,各显神通,但总是后劲不足,很多选手半途就相继夭折,闭门造车的蛮横者更是走不远,世界得天机者得对数,而这个幸运究竟会花落谁家呢?
文艺复兴时的巅峰期,自然科学帝国领域下的天文学混沌一片,经常遇到大量精密而又庞大的数值计算,于是数学家们为了避免烧脑计算量导致的频繁死亡事故,发明了对数“神器”,因此,对数可以说是应运而生,质子和合子的坎坷相遇就与对数的问世一样传奇。
首先想开启这扇对数之门的是德国的史蒂非,在1544年所著的《整数算术》中引入指数[1],但他徜徉在对数的门外,始终未能敲响对数概念的门,不管是“力道不足”还是“心有所属”,都让人实感惋惜。
继而是纳皮尔对数值计算日思夜想, 以寻求球面三角计算的简便为由,在1619年发表的《奇妙的对数表的描述》中阐明了对数原理,后人称为纳皮尔对数。这既不是自然对数[2]也不是常用对数[3],与现在用的对数之间也有梗,可记为Nap.㏒x,它与自然对数的关系为:Nap.㏒x=10㏑(107/x)。
天性迟钝的瑞士数学家彪奇也独立地发现了对数,可能发现得比纳皮尔还要早,但发表却比较迟。随后英国的布里格斯得到天恩眷顾,终于大功告成,在1624年创造了常用对数。1619年,伦敦的斯彼得也到天机,在先辈的基础上迈出新步伐,其所著的《新对数》使对数与自然对数更接近。由此,时机逐步成熟,待局势稳定时,对数函数成功得以创造,自然对数函数恋情的问世也将势在必行。就像质子的恋情一样,天时地利,自然人必合之。
综上,对数函数的发明者可谓是大功臣,简化了行星轨道的运算问题。正如科学家伽利略所说:给我时间、空间和对数,我可以创造出一个宇宙。又如十八世纪数学家拉普拉斯提到的:对数用缩短计算的时间来使天文学家的寿命加倍。对数函数的牛逼程度可见非同一般,才能得到大咖们如此夸赞。
传奇恋情的本真
自我属性
对数函数恋情与质子恋情进行阶段也十分相像。如质子男友合子,家境优渥,有足够的资本投资自己,事业步步攀登,似乎不费吹灰之力。在对数函数的恋情中,在a>1里,一路攀爬也毫不费力,在定义域上即为单调增函数。而且梦想x越大,越是显得自我y的能力越大,野心勃勃。
然而对于质子来说,家境有限,没有得天独厚的资本,只能靠自己一步步地向上攀爬。在竞争激烈的时代中,不进则退的道理人人适用,对数函数的恋情里,即0<a<1时,在定义域上即为单调减函数。而且梦想x越大,越是显得自身y的浩渺,但其依旧有着自我规划的路程。<>
感情如此好的一对,在事业上竟有如此大的差距,以至于最终无法逃离世俗的观念,家世、工作、前程难免总要被外人品头论足一番。有好事者常问两人谁比较优秀,这二人总异口同声,旗鼓相当,非你非我,正如在对数函数的恋情里,被问起奇偶性时,双方都称非奇非偶函数。
像吃了蜜糖般甜蜜的情侣们一样,质子和合子宣誓要一生一世在一起;而对数函数的恋情里面的宣誓也是如此饱含深情,表现在周期性,即不是周期函数。
情侣之间每每如此,当决定在一起的时候,质子和合子可以你我不分;在对数函数恋情的表达方式上,两者也都相当有骨气和个性,a>1或0<a<1的自我领域内,才会出现加减乘除混乱不清的局面,化抽象为有形即出现下列式子:<>
笔者观之,真心佩服在对数函数的恋情里,即便是如胶似漆,依旧保持本真自我,个性独立!
后记
质子和合子在生活里互相迁就与妥协,可谓是精神可佳,但纵然有五年你侬我侬的时间,却还是因为没有相同的家庭背景积淀,及截然不同的成长速度,造成了巨大的差距。当两个人相差距离遥远时,没有人会在原地等待,致使很多决定无法达成一致,分离势必成为结局。
而在对数函数的恋情里,纵然有x=1、y=0这样的交汇点,但最终还是因为a底蕴的不同,造成了渐行渐远的差距,分离也势必成为最终的结局。
纵然质子没有蓦然回首,那人就在灯火阑珊处的惊喜,但命运也绝对不会辜负质子这般对人生有规划的人;纵使现在伤心断肠,一切也都会成为过眼云烟,明天的美好行程即将开启.....
注释
[1]指数:在数学中代表着次方,是相同数字的乘法量变导致的质变产物。指数和对数是一对哲学范畴。
[2]自然对数:一般为lnX,就是以e为底数的对数。
[3]常用对数:以10为底的对数,用记号“lg”表示。
推荐书目
①《不可思议的自然对数》陈梅、陈仁政[著] 人民邮电出版社
②《牛顿教你学指数函数和对数函数》(韩)李智贤[著] 黄山书社